What is logic? Logic is an attempt to scientifically study and differentiate between valid and invalid arguments or statements. Arguments and statements are defined as containing a premise followed by a conclusion.
Logic is a way of understanding the world, and that has served humankind throughout its existence. In fact, it even pre-dates us. Over millions of years of evolution logic has been hard-wired into us, giving us technology ranging from more effective hunting tools to the modern-day computer. The liberal arts describes disciplines whose ultimate goal is to make sense of reality. As the study of logic does exactly this, it’s a perfect fit within a well-rounded liberal arts curriculum.
The Study of Logic Through the Ages – From the Great Philosophers to the Father of Computer Science
Logic has applications in essentially every field that seeks to express or understand the truth or reality, including everything from the arts and sciences to journalism, social movements, and human relationships.
Some of the most important logicians throughout the ages have included:
Aristotle (384-322 BC)
This Greek philosopher is credited with founding his namesake Aristotelian logic that defines a statement as being a premise followed by a conclusion; the foundation of logic today.
Al-Farabi (~872-~950)
Referred to as “the Second Teacher” in his time, with Aristotle being the first, al-Farabi expanded logic to encompass grammar and introduced the idea of subjective logic to accompany Aristotle’s simpler if-then proofs. He was born in either Afghanistan or Kazakhstan and died in Damascus. He bridged the gap between the Dark Ages and the Renaissance for Europe, preserving Aristotelian logic over that period in the Muslim world.
William of Ockham (~1287-1347)
This Franciscan friar from England is credited with introducing the principle of parsimony to logic. We know this today as his eponymous Occam’s razor, which states that when there are competing explanations for something, the most logical choice is the one with the fewest assumptions.
Alan Turing (1912-1954)
This British luminary is perhaps best known for being the progenitor of the field of computer science, based on his theories in logic, and as a corollary significantly contributing to the Allied victory in World War Two.
Because logic is instrumental in such a vast range of fields, it’s almost a requirement to study it in a broad liberal arts context.
Mathematics Follows Logic… and so Logic is Mathematic
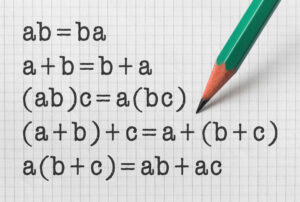It’s no coincidence that when you take an introductory philosophy course you’re going to cover what seems to be algebra in formulaic statements like: if a+b=d, and b+c=d, then a=c.
Philosophy looks a lot like math, and that’s because it is. Both can be defined as the expressions of a premise and a conclusion to ultimately determine valid and invalid arguments. This is pure Aristotelian logic, and it’s thanks to this that the study of mathematics has been able to progress.
Euclid immediately proceeded Aristotle, founding the field of what we know today as geometry. This was important for the advancement of mathematics. At this time algebra had not been well established; this would have happened later during the Islamic Golden Age. Instead, the closest the Greek world could come to algebra were general formulas based on geometry.
Aristotelian logic was widely accepted as being able to provide adequate solutions to mathematical problems all the way up until the 19th century when the German Gottlob Frege entered the scene. Though they had been around nearly as long as Aristotle himself, Frege was able to mathematically demonstrate the limits of Aristotelian logic by citing one of Euclid’s proofs that clearly and logically showed there were an infinite amount of prime numbers.
At this point mathematicians recognized the limits of Aristotelian logic and jumped aboard the Frege train, with many recognizing him as the greatest logician since Aristotle. Today Frege is credited with contributing early works on the topics of logic programming and artificial intelligence.
An interdisciplinary approach drawing from numerous civilizations, cultures, and religions that made the developments of mathematics possible, a story that’s best told by the liberal arts. And likewise the impact of mathematics on the future, in the form of computer science and AI, has molded key disciplines within the liberal arts.
Computer Science Owes its Existence to Protocols Based on Logic
The computer ranks among the top-five inventions of humanity thus far, competing with things like fire and agriculture. The computer as we know it today is a natural culmination of the millennia-old study of logic that was conceptualized in earnest by the British mathematician Alan Turing (1912-1954).
Earning his PhD in mathematics just before the outbreak of World War 2, Turing quickly put his skills to use leading successful efforts to decrypt secret communications between Axis Powers and turn the war in favor of the Allies. He took the lessons he learned as a cryptologist, which included early prototype computers, to found the fields of computer science and artificial intelligence.
During this time, he sketched a design for the first stored-program computer, the predecessor for what would eventually become the first personal computer or PC. The computer science field he helped to found was based entirely on mathematics, not least of which included mathematical logic, whose origins can be traced all the way back to Aristotelian logic.
Today we rely on computers to do everything from communicate with our friends to manage our global supply of food and energy. Without logic, none of these modern conveniences would be possible. Yet computers also raise new issues about fundamental human activities like socializing (social media), expression (freedom of speech), and the extent to which knowledge should be freely disseminated. These are reasons why it’s important to study logic in the context of the liberal arts.
Logic Even Expresses Itself Through Music
Typical discussions of logic will revolve around topics like math, the hard sciences, and computers. Subjects like music are usually left out of the stereotypical conversations about logic. But this need not be so.
While every culture has its own musical traditions, the Western music we’re familiar with –from Beethoven to Metallica to Justin Bieber to Beyoncé– follows specific rules of logic.
It’s all based on an eight-note scale (octave) that can be encompassed by 12 notes arranged in the same intervals that make up the major and minor keys from A to G. Three proportionally-spaced notes make up a chord, and Western music pleases the ear when chords follow a pre-determined key progression known as the circle of fifths.
Many Western songs follow the circle of fifths key progression, including:
- Bohemian Rhapsody by Queen
- Fly Me to the Moon by Frank Sinatra
- Beethoven’s 1st Movement from Piano Sonata number 8 in C minor
- Breaking Free from High School Musical
- Golden Slumbers by the Beatles
- Killing me Softly with His Song by the Fugees
- Take on Me by a-ha
- To Life from Fiddler on the Roof
Harmonics in music are also purely logical. When a musical note is understood to be a vibration at a specific frequency, harmonics are the overtones of notes reproduced at frequencies such as those that are ¼, ½, 2-times, and 4-times those of the note’s frequency. For example, a guitar’s A-string is tuned at 440 hertz (it vibrates 440 times each second). If you gently touch a guitar’s A-string in the middle it will divide it in half and vibrate at 880 hertz, an octave higher; a harmonic. Van Halen, No Doubt, Dire Straits, Pantera, and Ozzy Ozbourne are just a few of the musical artists that feature harmonics in some of their best-known hits.
The octave, the 12-tone scale, the circle of fifths, and harmonics are all formulaic constructions of music. Every culture has its own musical traditions that are subjective. This subjectivity aspect is open for interpretation by musicologists, but logicians have an easy time describing culturally-based musical norms within formulaic boundaries. The bridge between what’s cultural and what’s formulaic in music exemplify why the study of logic is augmented in the context of a liberal arts education, even in a subject like music where you’d least expect it.
